人工神经网络
版权声明:原创文章,未经授权,请勿转载
神经网络(Neural Network)是机器学习的一个分支,是一种模仿生物神经元结构的计算模型,也称为人工神经网络 (ANN)。
神经网络旨在从训练数据中学习模式和关系,不断调整和改进,并运用所学做出预测或决策。神经网络能够从复杂数据中提取有意义的信息来解决问题,与传统算法有着明显的不同。
基本结构
- 神经元: 是神经网络的基本单元,由输入、激活函数和输出组成。
- 输入层:接收原始数据(如图像像素、文本向量等)。
- 隐藏层:进行特征提取和转换(可能有多层,深度神经网络即由此得名)。
- 输出层:生成预测结果(如分类概率、回归值等)。
隐藏层与输出层由一个或多个神经元组成,这些神经元也被称为层的节点。
神经元
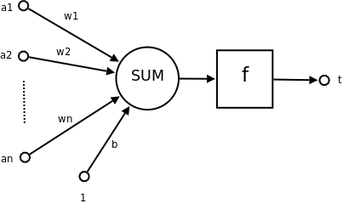
其中的符号含义为:
- $a1$ ~ $an$ 为神经元的输入,一般是一个向量的各个分量
- $w1$ ~ $wn$ 为神经元各个突触的权重值(weight)
- $b$ 为神经元的偏置(bias)
- $f$ 为激活函数,也称为传递函数,通常为非线性函数,本文中采用 $sigmoid$。
- $t$ 为神经元输出
可见,一个神经元的功能是求得输入向量与权向量的内积后,经一个非线性传递函数得到一个标量结果。
前向传播
前向传播是神经网络的核心计算过程,其目的是通过网络的权重和激活函数,将输入信号传递到输出层,得到预测结果。
我们通过最简单的前馈神经网络(Feedforward Network),来展示前向传播的过程。
神经网络的示意图如下:
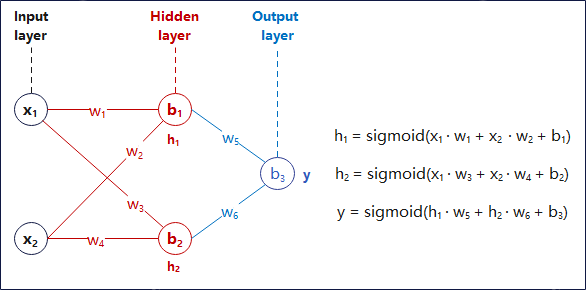
图 1-1: Feedforward Network
其中的符号含义为:
- $x_i$:输入层第i个节点的输入信号, 即样本的第i个特征值。
- $w_j$:各层的节点突触的权重值。
- $b_k$:各层的节点的偏置。
- $h_i$:隐藏层第i个节点的输出信号。
- $y$: 输出层的输出信号。
层的特征
- 输入层的节点数取决于输入数据的维度(即特征)的数量。
- 输入层数据的形状是(样本数, 特征数),可以输入一批样本,如果输入单个样本则为(1, 特征数)。
- 每一层权重的形状是(上一层节点数, 该层节点数)。
- 每一层偏置的形状是(1, 该层节点数)。
- 每一层输出的形状是(该层输入数据的行数【即样本数】, 该层节点数)。
数学表达
每个网络层(隐藏层和输出层),都可以视为一个拟合的函数,那么对于多层(深度)神经网络而言,它的数学本质,就等同于一个多层的复合函数: 它实现了从向量 $x$ 到向量 $y$ 的映射(如公式所示)
$$
y = h_3(h_2(h_1(x)))
$$
图 1-1 中神经网络的输入为 $x_1, x_2$ 输出的预测值为 $y$, 与实际值 $Y$ 的误差设为 $E$(也就是 损失函数), 则所有公式表示如下:
$$
\begin{aligned}
h_1 &= sigmoid(x_1 · w_1 + x_2 · w_2 + b_1) \\
h_2 &= sigmoid(x_1 · w_3 + x_2 · w_4 + b_2) \\
y &= sigmoid(h_1 · w_5 + h_2 · w_6 + b_3) \\
E &= \frac{1}{2}(y-Y)^2
\end{aligned}
$$
注意:
损失函数这里采用的是均方误差,而这里的 $\frac{1}{2}$ 是为了方便计算梯度而简化的,因为后面要乘以 $2$。
数据与计算过程
在实际的计算中,数据一般以矩阵的形式出现,这里演示前向传播时, 数据的运算过程以及中间结果的结构。
# 输入层数据, 形状 (3 样本数, 2 特征数)
X=[[x1, x2], # 样本1 特征向量
[x1, x2], # 样本2 ...
[x1, x2]] # 样本3
# 隐藏层权重, 形状 (2 上一层节点数, 2 隐藏层节点数)
# h1, h2
Hw=[[w1, w3],
[w2, w4]]
# 计算隐藏层的输入数据(输入向量与隐藏层权重的点积)
# Hi=np.dot(X, Hw)
Hi=[[x1·w1 + x2·w2, x1·w3 + x2·w4], # 样本1
[x1·w1 + x2·w2, x1·w3 + x2·w4], # ...
[x1·w1 + x2·w2, x1·w3 + x2·w4]]
# 隐藏层偏置, 形状 (1, 2 隐藏层节点数)
Hb=[[b1, b2]]
# 计算隐藏层的输出数据(隐藏层输入数据与隐藏层偏置的加和后再通过激活函数处理)
# Ho=sigmoid(Hi+Hb)
Ho=[[h1=sigmoid(x1·w1 + x2·w2 + b1), h2=sigmoid(x1·w3 + x2·w4 + b2)], # 样本1
[h1=sigmoid(x1·w1 + x2·w2 + b1), h2=sigmoid(x1·w3 + x2·w4 + b2)], # ...
[h1=sigmoid(x1·w1 + x2·w2 + b1), h2=sigmoid(x1·w3 + x2·w4 + b2)]]
# 化简后以 h1, h2 代替
Ho=[[h1, h2],
[h1, h2],
[h1, h2]]
# 输出层权重, 形状 (2 上一层节点数, 1 输出层节点数)
Ow=[[w5],
[w6]]
# 输出层偏置, 形状 (1, 1 输出层节点数)
Ob=[[b3]]
# 计算输出层输出值, 也就是神经网络的预测值
# Oo=np.dot(Ho, Ow) + Ob
Oo=[[sigmoid(h1·w5 + h2·w6 + b3)], # 样本1
[sigmoid(h1·w5 + h2·w6 + b3)], # 样本2
[sigmoid(h1·w5 + h2·w6 + b3)]] # 样本3
y=Oo
观察以上数据可以得出:
- 输入数据与中间数据中,每一行都表示一个样本,而列则表示该样本的某一个特征的信息。
- 网络各个层的权重与偏置数据中,每一列表示的是该层节点的数据, 而行则与上一层的节点一一对应(这特性是由于矩阵乘法的性质决定)。
反向传播
为了训练神经网络, 我们使用反向传播(Backpropagation)算法, 从输出到输入反向计算并更新每一层的权重和偏置, 从而让神经网络的输出值与实际值的误差最小化。
我们首先需要计算 误差 $E$ 关于每一个权重与偏置的梯度(偏导数),即该权重或偏置对误差的贡献度。
然后再根据 梯度下降法(Batch Gradient Descent)来更新。
1. 计算与更新权重 $w_5$
1.1 $w_5$ 对 $E$ 的贡献, 表示为 $\frac{\partial E}{\partial w_5}$。
1.2 为了方便后面的计算, 我们将公式中的 $sigmoid$ 函数的输入提取出来:
$$
\begin{aligned}
c &= h_1 · w_5 + h_2 · w_6 + b_3 \\
y &= sigmoid(c) \\
E &= \frac{1}{2}(y-Y)^2
\end{aligned}
$$
1.3 根据导数的链式法则, 可以得到:
$$
\frac{\partial E}{\partial w_5} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial c} \cdot \frac{\partial c}{\partial w_5}
$$
1.4 分别计算各项:
$$
\begin{aligned}
\frac{\partial E}{\partial y} &= y-Y \\
\frac{\partial y}{\partial c} &= \text{sigmoid_derivative}(c) \\
\frac{\partial c}{\partial w_5} &= h_1 \\
\end{aligned}
$$
1.5 得到:
$$
\frac{\partial E}{\partial w_5} = (y-Y) \cdot \text{sigmoid_derivative}(c) \cdot h_1
$$
- 由于 $h_1$、$c$、$y$ 都在前向传播计算过程中计算过, 因此我们可以直接使用从而计算出结果。
1.6 更新权重:
$$
w_5 = w_5 - η \cdot \frac{\partial E}{\partial w_5}
$$
- 其中 $η$ 表示学习率,也称为步长或学习速率,这里取 $0.1$。
2. 计算与更新权重 $w_1$
2.1 同理, 误差贡献表示为: $\frac{\partial E}{\partial w_1}$
2.2 提取:
$$
\begin{aligned}
a &= x_1 · w_1 + x_2 · w_2 + b_1 \\
h_1 &= sigmoid(a) \\
c &= h_1 · w_5 + h_2 · w_6 + b_3 \\
y &= sigmoid(c) \\
E &= \frac{1}{2}(y-Y)^2
\end{aligned}
$$
2.3 链式法则代入:
$$
\frac{\partial E}{\partial w_1} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial c} \cdot \frac{\partial c}{\partial h_1} \cdot \frac{\partial h_1}{\partial a} \cdot \frac{\partial a}{\partial w_1}
$$
2.4 分别计算:
$$
\begin{aligned}
\frac{\partial E}{\partial y} &= y-Y \\
\frac{\partial y}{\partial c} &= \text{sigmoid_derivative}(c) \\
\frac{\partial c}{\partial h_1} &= w_5 \\
\frac{\partial h_1}{\partial a} &= \text{sigmoid_derivative}(a) \\
\frac{\partial a}{\partial w_1} &= x_1 \\
\end{aligned}
$$
2.5 得到:
$$
\frac{\partial E}{\partial w_1} = (y-Y) \cdot \text{sigmoid_derivative}(c) \cdot w_5 \cdot \text{sigmoid_derivative}(a) \cdot x_1
$$
2.6 更新权重:
$$
w_1 = w_1 - η \cdot \frac{\partial E}{\partial w_1}
$$
3. 计算与更新偏置 $b_1$
3.1 同理, 误差贡献表示为: $\frac{\partial E}{\partial b_1}$
3.2 提取:
$$
\begin{aligned}
a &= x_1 · w_1 + x_2 · w_2 + b_1 \\
h_1 &= sigmoid(a) \\
c &= h_1 · w_5 + h_2 · w_6 + b_3 \\
y &= sigmoid(c) \\
E &= \frac{1}{2}(y-Y)^2
\end{aligned}
$$
3.3 链式法则代入:
$$
\frac{\partial E}{\partial b_1} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial c} \cdot \frac{\partial c}{\partial h_1} \cdot \frac{\partial h_1}{\partial a} \cdot \frac{\partial a}{\partial b_1}
$$
3.4 分别计算:
$$
\begin{aligned}
\frac{\partial E}{\partial y} &= y-Y \\
\frac{\partial y}{\partial c} &= \text{sigmoid_derivative}(c) \\
\frac{\partial c}{\partial h_1} &= w_5 \\
\frac{\partial h_1}{\partial a} &= \text{sigmoid_derivative}(a) \\
\frac{\partial a}{\partial b_1} &= 1 \\
\end{aligned}
$$
3.5 得到:
$$
\frac{\partial E}{\partial b_1} = (y-Y) \cdot \text{sigmoid_derivative}(c) \cdot w_5 \cdot \text{sigmoid_derivative}(a)
$$
3.6 更新权重:
$$
b_1 = b_1 - η \cdot \frac{\partial E}{\partial b_1}
$$
Python 实现
为了简化矩阵的计算, 这里我们使用了numpy 模块, numpy 是一个开源的Python库, 广泛用于科学计算。
首先定义一个神经网络类, 主要包含两个函数, 一个是前向传播函数, 一个是反向传播函数。
import numpy as np
# 定义激活函数及其导数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return x * (1 - x)
# 定义神经网络类
class FeedNeuralNetwork:
def __init__(self, input_size, hidden_size, output_size):
# 初始化权重和偏置
self.weights1 = np.random.randn(input_size, hidden_size) # 输入层到隐藏层的权重
self.bias1 = np.zeros((1, hidden_size)) # 隐藏层的偏置
self.weights2 = np.random.randn(hidden_size, output_size) # 隐藏层到输出层的权重
self.bias2 = np.zeros((1, output_size)) # 输出层的偏置
def forward(self, X):
# 前向传播
self.hidden_input = np.dot(X, self.weights1) + self.bias1 # 隐藏层输入
self.hidden_output = sigmoid(self.hidden_input) # 隐藏层输出
self.final_input = np.dot(self.hidden_output, self.weights2) + self.bias2 # 输出层输入
self.final_output = sigmoid(self.final_input) # 输出层输出
return self.final_output
def backward(self, X, Y, learning_rate):
# 反向传播
m = X.shape[0] # 样本数量
# 输出层误差
output_error = self.final_output - Y # 误差函数: 求的是每个样本的误差 #(∂E/∂y)
output_delta = output_error * sigmoid_derivative(self.final_output) #(∂E/∂y * ∂y/∂c)
# 隐藏层误差
hidden_error = np.dot(output_delta, self.weights2.T) #(∂E/∂y * ∂y/∂c * ∂c/∂h_1)
hidden_delta = hidden_error * sigmoid_derivative(self.hidden_output) #(∂E/∂y * ∂y/∂c * ∂c/∂h_1 * ∂h_1/∂a)
# 更新权重和偏置
# self.hidden_output.T 表示隐藏层输出, 也就是: h_1, h_2, 又分别等于 ∂c/∂w_5, ∂c/∂w_6 (见反向传播公式)
# 因此这里相当于:
# - ∂E/∂w_5 = ∂E/∂y * ∂y/∂c * ∂c/∂w_5
# - ∂E/∂w_6 = ∂E/∂y * ∂y/∂c * ∂c/∂w_6
# 关于转置的原因:
# - hidden_output 的形状为 (样本数, 2)
# - 第一列表示 h_1
# - 第二列表示 h_2
# - output_delta 的形状为 (样本数, 1)
# - 转置一方面, 可以使两个矩阵符合矩阵乘法的要求, 另一方面是, 可以同时更新 weights2 中的权重 (w_5, w_6)
# 关于最后除以样本数(/m)的原因:
# - 执行矩阵乘法后, 结果矩阵的形状为 (2, 1), 也就是说这批样本的误差之和, 因此需要除以样本数才能得到权重的更新量
#
self.weights2 -= learning_rate * np.dot(self.hidden_output.T, output_delta) / m
self.bias2 -= learning_rate * np.sum(output_delta, axis=0, keepdims=True) / m
self.weights1 -= learning_rate * np.dot(X.T, hidden_delta) / m
self.bias1 -= learning_rate * np.sum(hidden_delta, axis=0, keepdims=True) / m
def train(self, X, Y, epochs, learning_rate, verbose=False):
losses = []
for epoch in range(epochs):
output = self.forward(X)
self.backward(X, Y, learning_rate)
# 打印损失
if epoch % 100 == 0:
loss = np.mean(np.square(Y - output))
if verbose and epoch % 1000 == 0:
print(f"Epoch {epoch}, Loss: {loss}")
losses.append(loss)
return losses
随机生成一组二分标签,作为训练数据,来训练并测试:
# 生成一些简单的训练数据, 100个样本,每个样本有2个特征
X = np.random.randn(100, 2)
Y = (X[:, 0] + X[:, 1] > 0).astype(int).reshape(-1, 1)
T = np.array([[0.5, 0.5], [-0.5, -0.5], [0.1, -0.3], [-0.2, 0.4]])
# 定义包含2个节点的隐藏层的神经网络
nn = FeedNeuralNetwork(input_size = 2, hidden_size = 2, output_size = 1)
# 训练神经网络
nn.train(X, Y, epochs=10000, learning_rate=0.1, verbose=True)
# 测试神经网络
predictions = nn.forward(T)
print("Predictions for test data:\n", predictions)
Epoch 0, Loss: 0.2832618264020293
Epoch 1000, Loss: 0.19258215420098243
Epoch 2000, Loss: 0.0962378267167891
Epoch 3000, Loss: 0.061623524890982315
Epoch 4000, Loss: 0.04722564099421363
Epoch 5000, Loss: 0.03931114517521166
Epoch 6000, Loss: 0.034210231243449074
Epoch 7000, Loss: 0.03059331500272531
Epoch 8000, Loss: 0.027863796066633327
Epoch 9000, Loss: 0.025712263913194387
Predictions for test data:
[[0.97895248]
[0.03954089]
[0.22193466]
[0.76031685]]
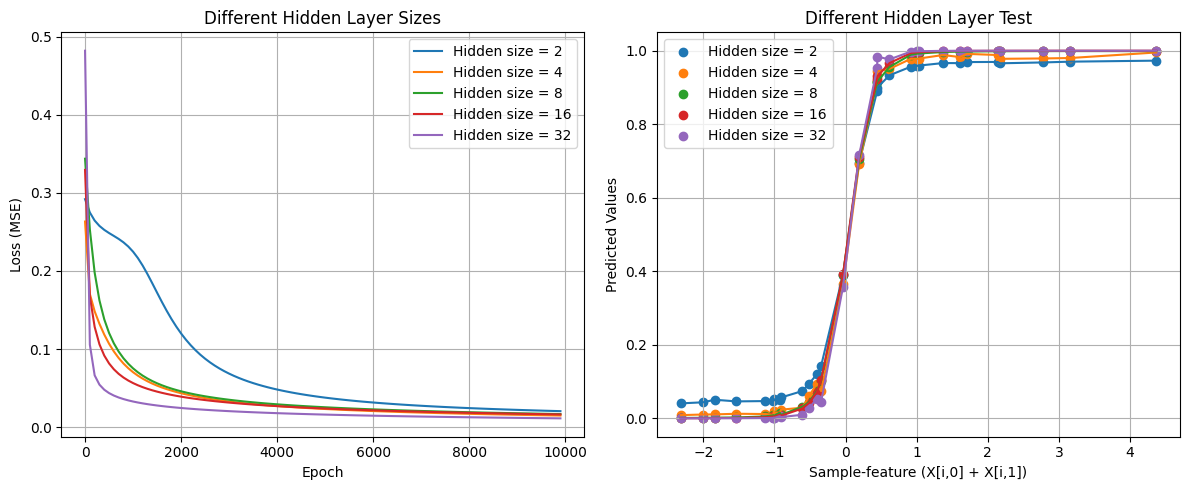
测试不同隐藏层节点数量之间的差异,主要从训练损失曲线和预测结果两个方面进行比较。
import matplotlib.pyplot as plt
# 生成一些简单的训练数据, 100个样本,每个样本有2个特征
np.random.seed(42)
X = np.random.randn(100, 2)
Y = (X[:, 0] + X[:, 1] > 0).astype(int).reshape(-1, 1)
T = np.concatenate((np.array([[0.5, 0.5], [-0.5, -0.5]]), np.random.randn(28, 2)), axis=0)
# 训练数据排序, 避免画图时画错序
T = T[np.argsort(T.sum(axis=1))]
# colors = ["blue", "green", "orange", "red", "purple", "brown", "pink", "gray"]
colors = ['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728', '#9467bd', '#8c564b', '#e377c2', '#7f7f7f', '#bcbd22', '#17becf']
epochs = 10000
sequence = [2, 4, 8, 16, 32]
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
predictions = []
for i, size in enumerate(sequence):
nn = FeedNeuralNetwork(2, size, 1)
losses = nn.train(X, Y, epochs, learning_rate=0.1)
x_axis = np.arange(0, epochs, 100)
plt.plot(x_axis, losses, label=f'Hidden size = {size}', color=colors[i])
predictions.append(nn.forward(T).flatten())
# 左侧:训练损失曲线
plt.title('Different Hidden Layer Sizes')
plt.xlabel('Epoch')
plt.ylabel('Loss (MSE)')
plt.legend()
plt.grid(True)
# # 右侧:预测结果对比
plt.subplot(1, 2, 2)
x_values = T.sum(axis=1)
for i, t in enumerate(predictions):
plt.scatter(x_values, t, c=colors[i], marker='o', label=f'Hidden size = {sequence[i]}')
plt.plot(x_values, t, colors[i])
plt.title('Different Hidden Layer Test')
plt.xlabel('Sample-feature (X[i,0] + X[i,1])')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

Comments ()