聚类 k-means

K-means (K平均聚类) 是一种常用的无监督学习算法，主要用于聚类分析。其目标是将数据集划分为 K 个簇，使得每个数据点归属于最近的簇中心，且簇内数据点尽可能相似，簇间差异尽可能大。

特点：

• 简单易用，广泛应用于图像分割、市场细分、文档聚类等领域。。
• 需预先设定 K 值，选择不当可能影响结果。
• 对初始中心敏感，可能陷入局部最优。
• 对噪声和异常值敏感。

K-means 算法步骤：

1. 初始化 K 个中心点（ centroids ）。
2. 将每个数据点分配到最近的中心点所属簇中。
3. 更新每个簇的中心点，使其成为其所有数据点的平均值。
4. 重复步骤 2 和步骤 3，直到簇中心不再移动或达到最大迭代次数。

实例

首先，我们生成一些随机数据，然后使用 KMeans 算法对它们进行聚类，并使用 matplotlib 绘制出聚类结果。

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置随机数种子
np.random.seed(None)

# 生成 100 个二维数据点，范围在 [0, 50]
data = np.random.randint(0, 50, (100, 2)).astype(np.float32)

# 定义 K 值（簇的数量）
K = 3

# 定义 K-means 的停止条件, 两个标识符 通过 + 来组合, 类似于 |
#  - TERM_CRITERIA_MAX_ITER: 最大迭代次数条件，达到指定次数时停止迭代
#  - TERM_CRITERIA_EPS: 精度条件，簇中心的移动幅度小于阈值（精度）时停止迭代
criteria = (cv2.TERM_CRITERIA_MAX_ITER + cv2.TERM_CRITERIA_EPS, 10, 1.0)

# 运行 K-means 算法
#   - attempts: 重复算法次数, 返回紧凑性最好的一次结果
#   - flags: 初始中心的选择方法, 这里采用随机选择
#   - 返回值: 
#     - compactness: 表示结果的紧凑性, 即所有数据点到其所属簇中心的距离的平方和
#     - labels: 表示每个数据点所属的标签(簇)的索引, 形状为 (N, 1): [ [lebel_id], [lebel_id], ... ]
#     - centers: 表示每个簇的中心
# 参考: https://docs.opencv.org/4.11.0/d5/d38/group__core__cluster.html#ga9a34dc06c6ec9460e90860f15bcd2f88
compactness, labels, centers = cv2.kmeans(data, K, None, criteria, attempts=10, flags=cv2.KMEANS_RANDOM_CENTERS)

# 将数据点按标签分离, 使用 NumPy 的布尔索引操作
cluster1 = data[labels.ravel() == 0]
cluster2 = data[labels.ravel() == 1]
cluster3 = data[labels.ravel() == 2]

# 使用 Matplotlib 可视化结果
# 展示原始数据点
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)  # 1 行 2 列，第 1 个子图
plt.scatter(data[:, 0], data[:, 1], c='blue', label='Data Points') # data[:, 0] 所有点的 X 坐标集, NumPy 多维切片语法
plt.ylabel('Y')
plt.title('Original Data Points')
plt.legend()

# 展示聚类结果
plt.subplot(1, 2, 2)  # 1 行 2 列，第 2 个子图 
plt.scatter(cluster1[:, 0], cluster1[:, 1], c='blue', label='Cluster 1')
plt.scatter(cluster2[:, 0], cluster2[:, 1], c='green', label='Cluster 2')
plt.scatter(cluster3[:, 0], cluster3[:, 1], c='red', label='Cluster 3')
plt.scatter(centers[:, 0], centers[:, 1], s=200, c='black', marker='*', label='Centers')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('K-means Clustering with OpenCV')
plt.legend()
plt.show()

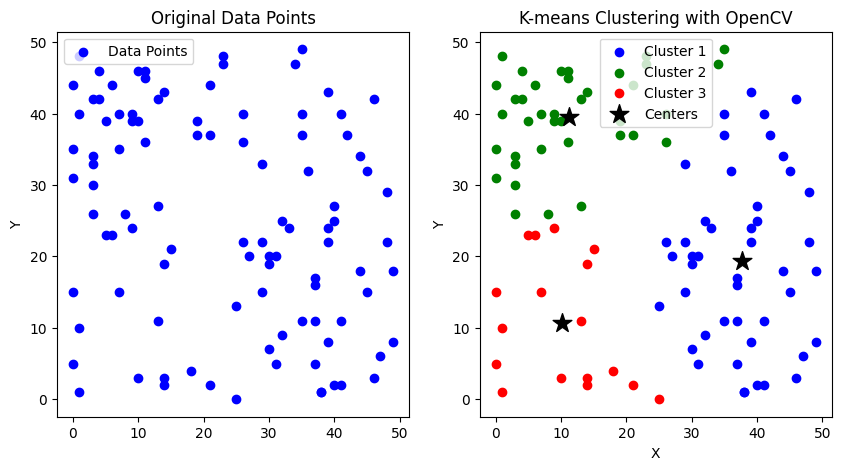
从结果图中可以看到，所有点都都被聚成了 3 个簇，以颜色区分。

K 的取值与聚类效果

K 的取值以及中心的的初始化方式，对聚类效果影响很大。我们可以通过下面的案例观察不同的 K 值与紧凑性（WCSS - Within Cluster Sum of Squares）的关系。

import cv2
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(None)

# 生成 4 个簇的数据
data = np.concatenate([
    np.random.normal(loc=center, scale=2, size=(25, 2))
    for center in [[0, 0], [10, 10], [0, 10], [10, 0]]
]).astype(np.float32)

# 定义 K 值范围
K_values = range(1, 11)
compactness_values = []

# 定义 K-means 的停止条件
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# 对每个 K 值运行 K-means
for K in K_values:
    # 运行 K-means
    compactness, labels, centers = cv2.kmeans(data, K, None, criteria, 10, cv2.KMEANS_RANDOM_CENTERS)
    compactness_values.append(compactness)  # 记录紧凑性

# 展示原始数据点
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)  # 1 行 2 列，第 1 个子图
plt.scatter(data[:, 0], data[:, 1], c='blue', label='Data Points') # data[:, 0] 所有点的 X 坐标集, NumPy 多维切片语法
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Original Data Points')
plt.legend()

# 绘制 K 值与紧凑性的关系图
plt.subplot(1, 2, 2)
plt.plot(K_values, compactness_values, marker='o', linestyle='-', color='b')
plt.xlabel('K (Number of Clusters)')
plt.ylabel('WCSS (Compactness)')
plt.title('K vs WCSS (OpenCV)')
plt.xticks(K_values)
plt.grid(True)
plt.show()

通过上面的曲线图，我们可以看出当 K 值越大，紧凑性（WCSS）的度量值越低，曲线整体上像是一个胳膊肘的形状。 而当 K 值达到某个值时（曲线的肘点），折线的下降趋势开始显著降低，这个位置就是 K 的最佳值，因此这种方法也称为 肘点法（Elbow method）。

参考

• Visualizing K-Means Clustering
• 视频演示: k-means算法聚类过程